

MHDuet is an automatically generated, efficient computational code with distributed adaptive mesh refinement (AMR) which solves strongly gravitating, high density matter to study the dynamics of compact objects (i.e., black holes and neutron stars) in different astrophysical scenarios.
MHDuet solves the Einstein equations coupled to the general-relativistic magnetohydrodynamics equations to evolve consistently self-gravitating, magnetized matter that constitute neutron stars. The matter is modeled as a perfect fluid with several forms of equation of state, including microphysical tabulated ones. It employs Large Eddy Simulations (LES) techniques, with the gradient Sub-Grid Scale model, to capture small scale dynamics that might develop in scenarios involving neutron star mergers and/or accretion disks. The code also incorporates different treatments to solve the neutrino transport equations. Currently it uses a leakage scheme for neutrino cooling, soon to be upgraded to an M1 formalism with the grey approximation.
The parallelization and distributed AMR are handled by the publicly available
AMReX infrastructure, which scales well on both CPU and GPU architectures.
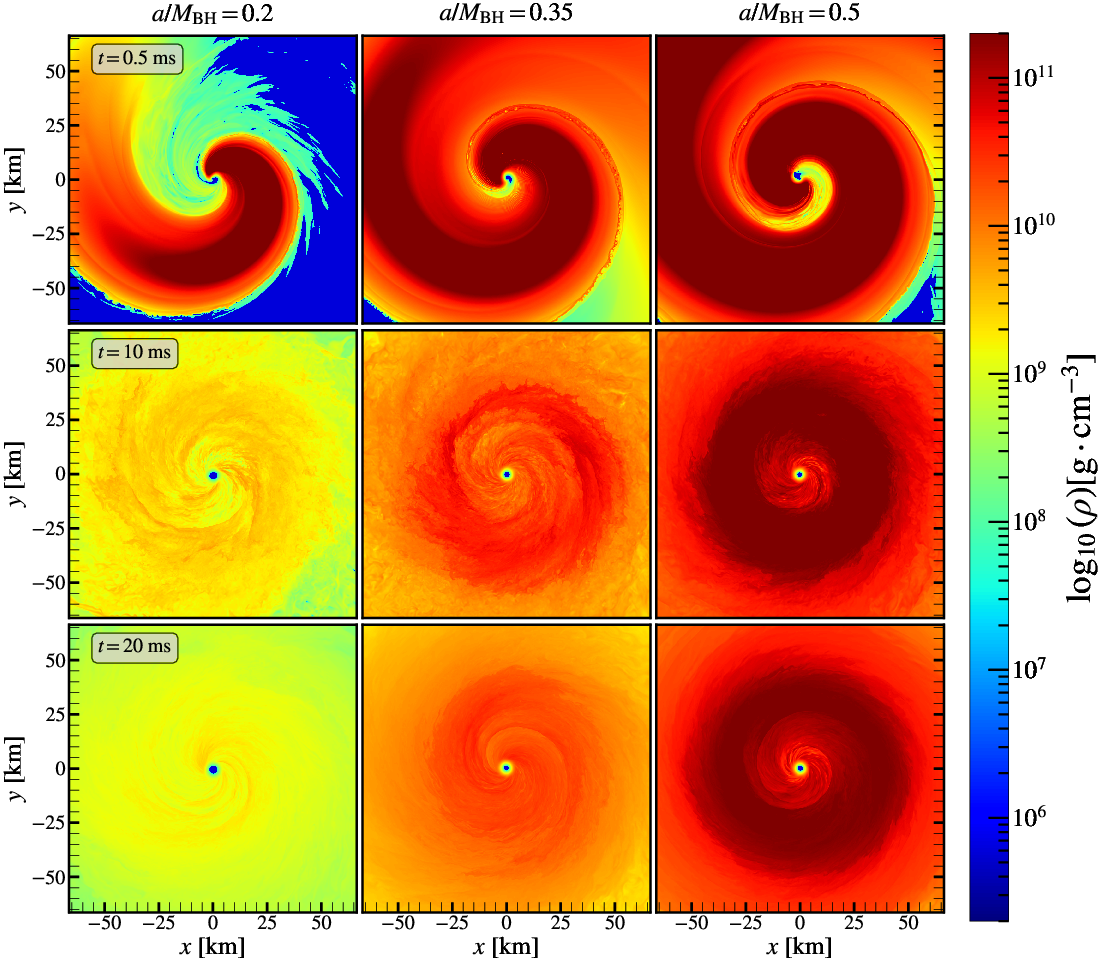
A neutron star merges with a black hole in [20].
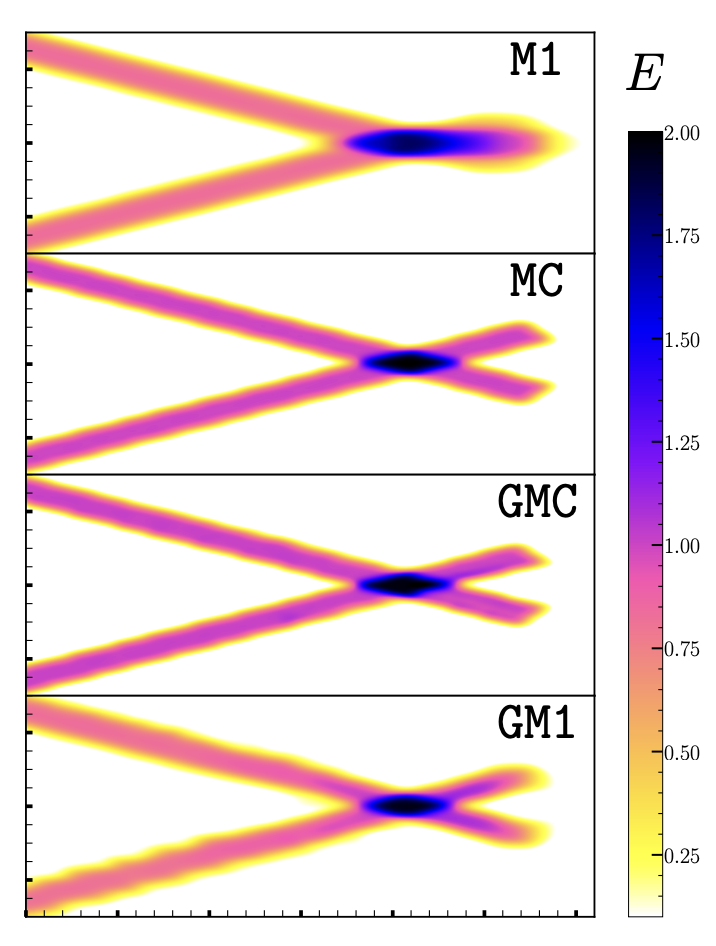
Colliding neutrino beams in [18].
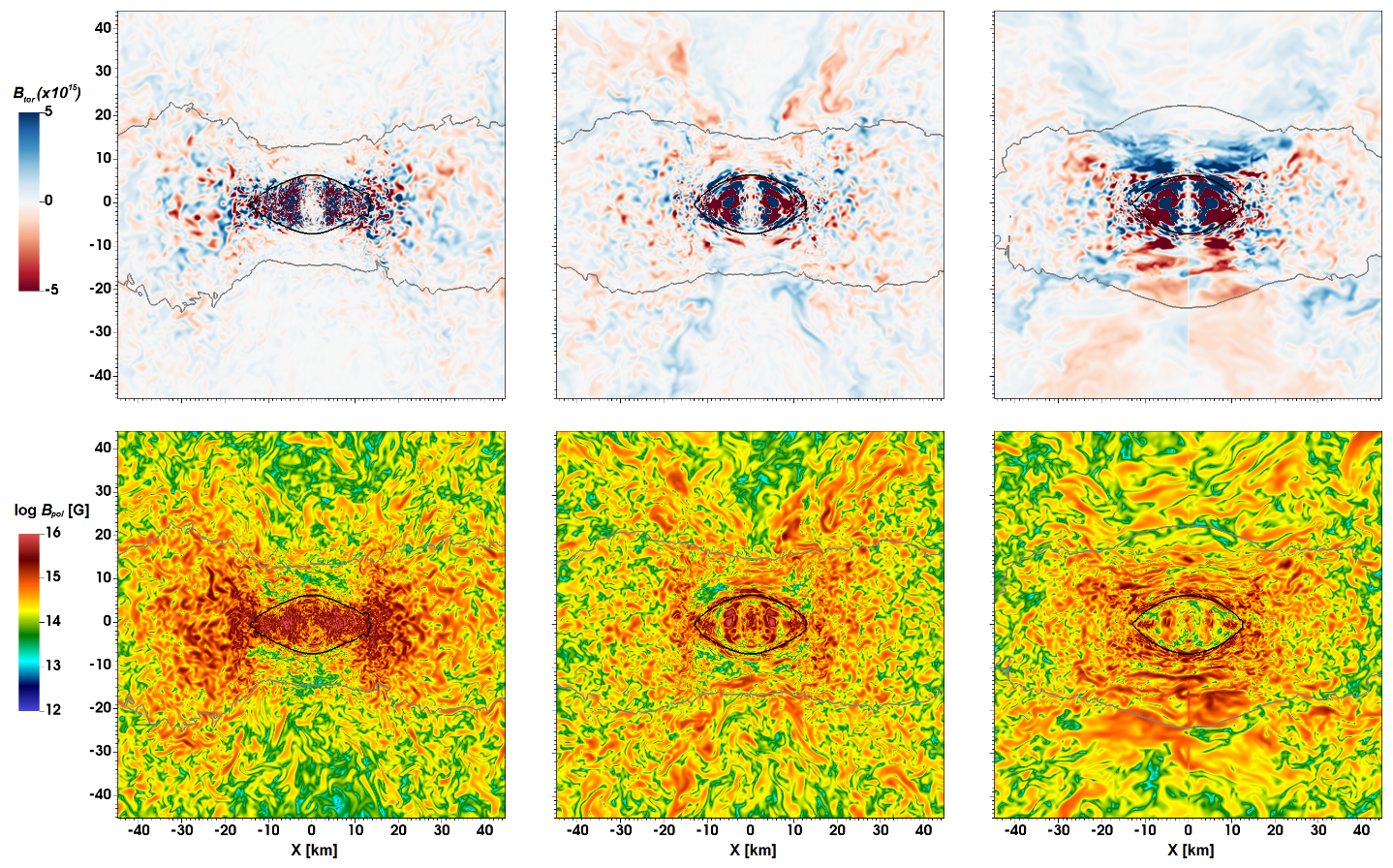
Magnetic field growth due to turbulent dynamics and MHD instabilities produced during the merger of binary neutron stars. Toroidal (top row) and norm of the poloidal (bottom row) components of the magnetic field in the meridional plane at times t = (15, 50, 110) ms after the merger. Persistent large-field structures, with a ”teddy bear face” shape, are being formed in the bulk for the toroidal component. More about this project can be found in [15].
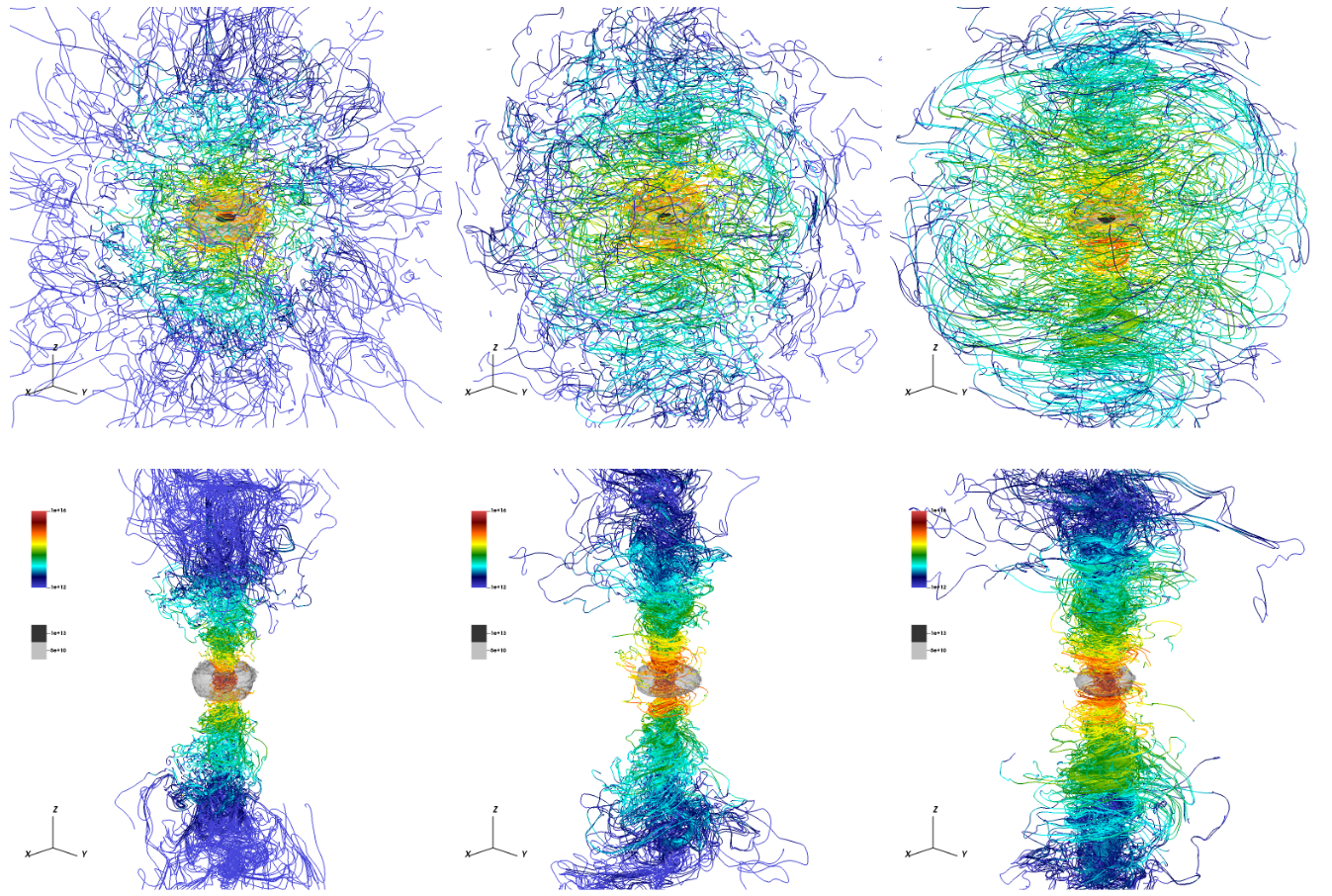
Formation of magnetically dominated jets in hypermassive neutron stars produced by a binary merger. Streamlines of the magnetic field, at times t = (15, 50, 110) ms after the merger, together with a density constant surface. Notice the helical jet-like structure developing during the post-merger phase. More about this project can be found in [15].
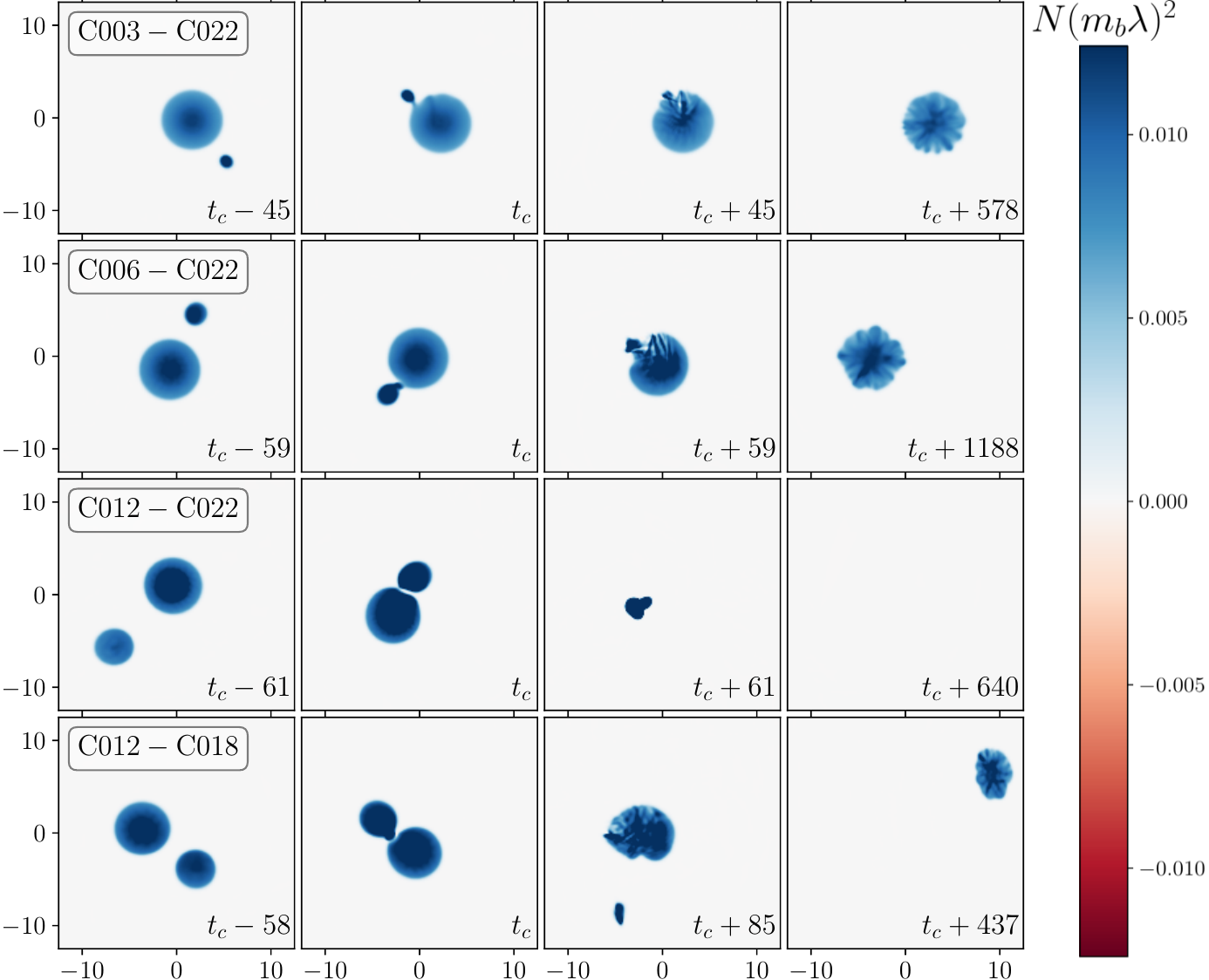
Coalescence of a type of Exotic Compact Object, described by a complex scalar field, known as a boson star. Noether charge densities in the equatorial plane (z = 0) at representative times from the merger of unequal mass, highly compact boson stars. The two first rows form a massive non-rotating boson star after the merger. The third case forms a spinning black hole. The latest case ejects matter as a blob with a significant kick velocity (up to a few 100 km/s), which could produce wandering remnant boson stars. More about this project can be found in [11].
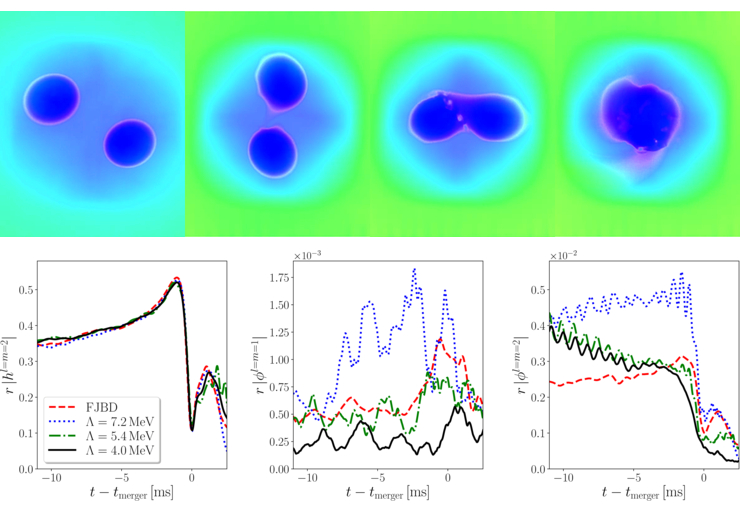
Coalescence of binary neutron stars in alternative gravity theories. K-essence is a cosmologically relevant scalar-tensor theory that involves first-order derivative self-interactions, which pass all existing gravitational wave bounds and provide a screening mechanism. Here, we study the effects of this kinetic screening in binary neutron stars. In the top panel, the different time snapshots show the evolution of the scalar field that develops a common “envelope” around the fluid density. The scalar and gravitational radiation for different representative cases are shown in the bottom panel. More about this project can be found in [9].
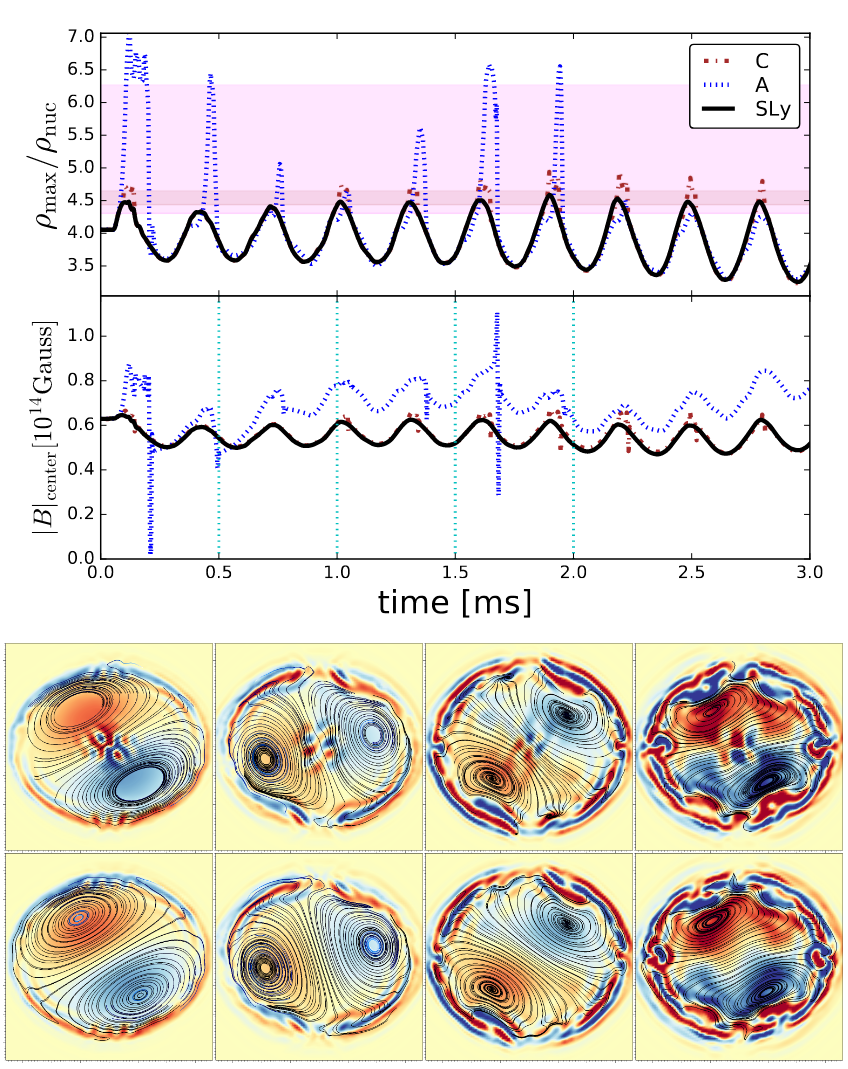
A phase transition at very high densities are expected for theoretical reasons, and neutron star mergers may produce sufficiently dense material to reveal such a transition observationally. A magnetized, rotating star evolved with various equations of state that include possible phase transitions. The peak density goes into and out of the phase transition. The magnetic structure of the core depends on the existence of the phase transition, although it's not clear if such differences could propagate to the stellar surface. From [8].
Access research papers for in-depth information.
Although this code is automatically generated using Simflowny, you need not install it. Instead, you might need to install MPI (OpenMPI => 1.10.2), the libraries that support I/O (HDF5 and Silo), the infrastructure providing parallelization and AMR (SAMRAI or AMReX) and the libraries for compact-objects initial data (Lorene or FUKA). More detailed instructions can be found in this Simflowny webpage.
Pre-requisites installation instructions
Version 2.0 of MHDuet for AMReX can be downloaded here: mhduet-2.0.tgz (un-tarred here) with the corresponding version for boson star evolution here: mhduetBS-2.0.tgz (un-tarred here)
Compiling instructions
The scaling tests are performed using the Boson star code. It solves a single boson star by using a fourth order RK to evolve in time, 4th order finite difference to discretize the spatial derivatives and a 6th order Kreiss-Oliger dissipation to damp the high-frequency noise.
We have considered three different versions of the code: AMReX-GPU, AMReX-CPU and SAMRAI (i.e., only CPU). The CPU runs have been performed in MareNostrum 4 (1 node=48 cores), while that the GPU runs have been perfomed in Tursa (1 node = 4 GPUs NVIDIA A100-40), Frontera (1 node = 4 GPUs NVIDIA Quadro RTX 5000) and MareNostrum 5 (1 node = 4 GPUs NVIDIA Hopper H100 64GB HBM2).
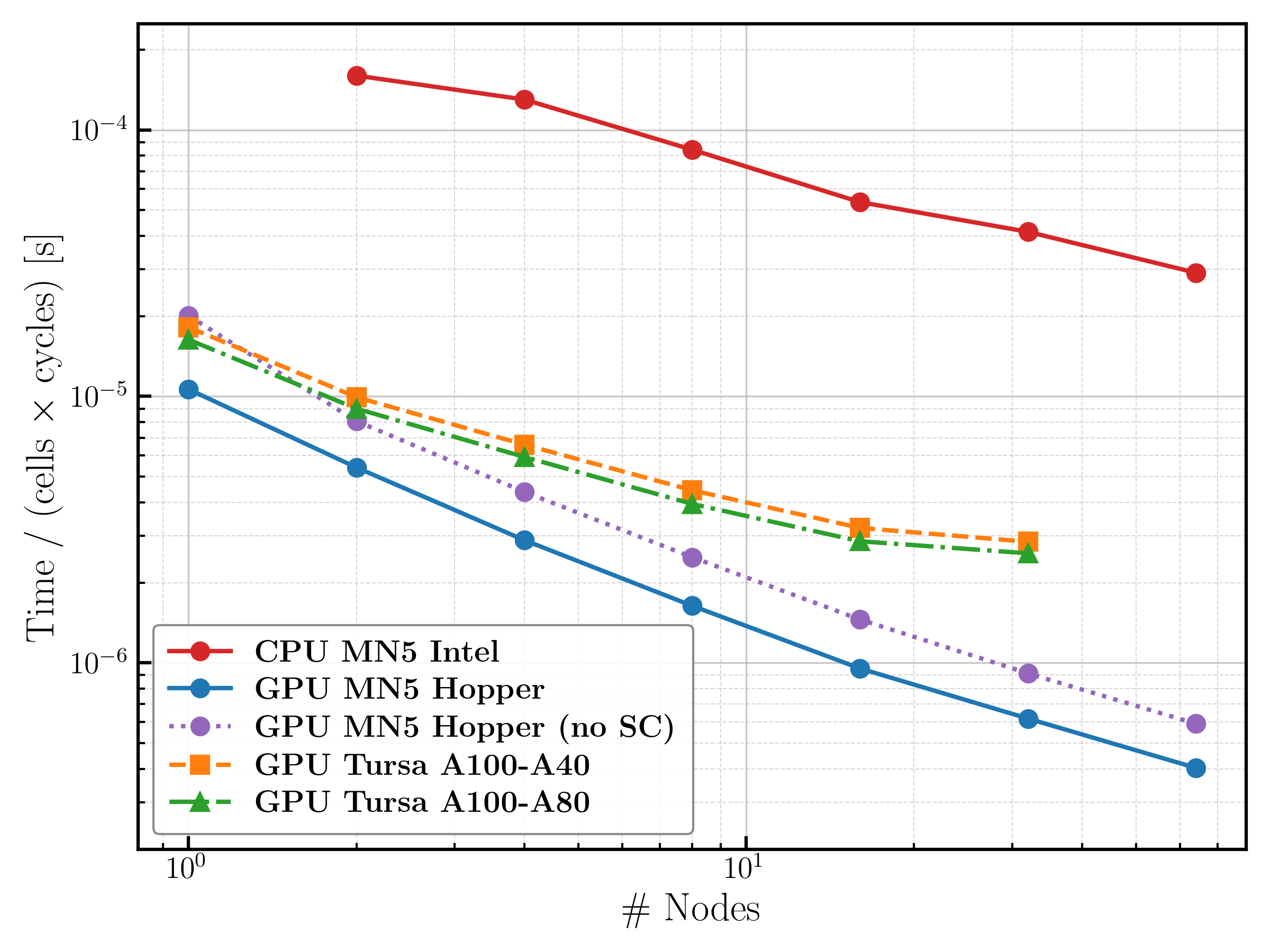
Strong scaling with the single, rotating, hot NS using the DD2 tabulated EoS. The CPU scaling suffers because a large fraction of the available memmory is employed saving the tabulated EoS. The GPU-MN5 is at least 20 times faster than CPU-MN5.
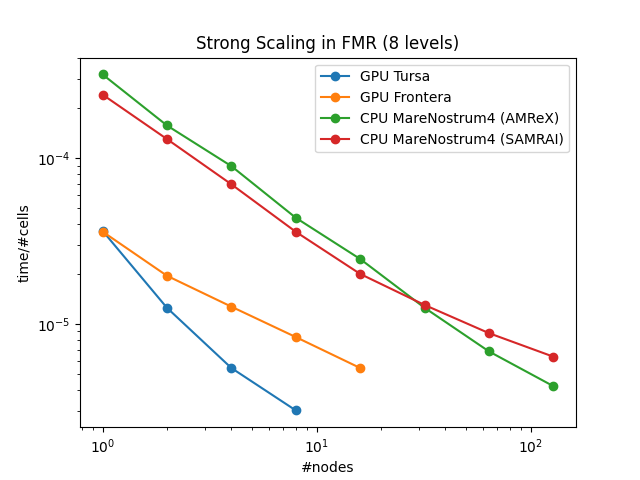
Simulation of a boson star in a domain with a coarse grid + 7 FMR levels, using subcycling in time. Notice that the SAMRAI infrastructure does not scale strongly for this problem beyond 16 nodes. Again, simulations run with GPUs are significantly faster than the CPU ones.
Find scripts for different analysis for hdf5 data in scripts
The evolution equations and the numerical methods implemented in MHDuet can be found in Ref. [23]. The equations for the boson star version can be found in Ref. 1705.01071.
A general description of the parameters and structure of the codes are documented here for SAMRAI (download) and AMReX (download). The parameters related to SAMRAI are further documented here.
Find answers to frequently asked questions and common standard errors.